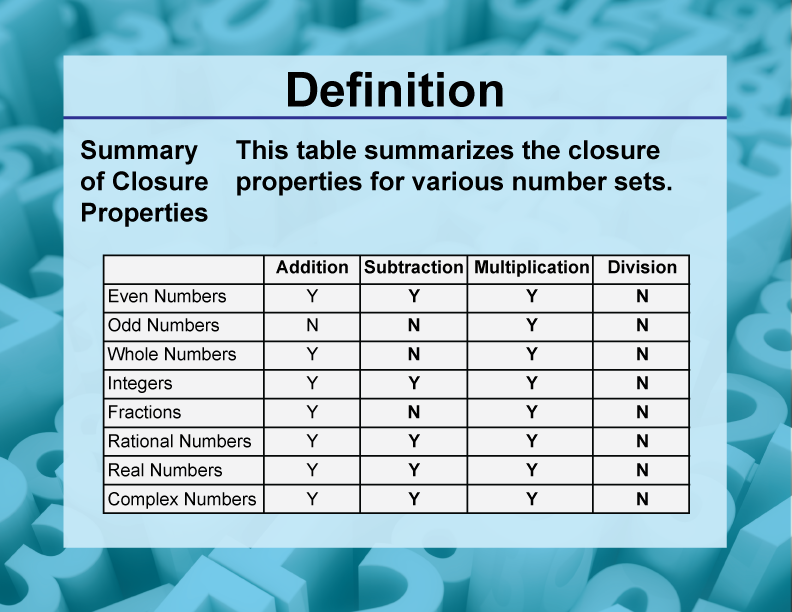
Define Closure Property In Math - In mathematics, closure refers to the likelihood of an operation on elements of a set. If something is closed, then it means if an operation is. What is the closure property? Closure property of whole numbers under addition: Closure property holds for addition and multiplication of whole numbers. The closure property of addition for real numbers states that if a and b are real numbers, then a + b is a unique.
Closure property of whole numbers under addition: If something is closed, then it means if an operation is. In mathematics, closure refers to the likelihood of an operation on elements of a set. The closure property of addition for real numbers states that if a and b are real numbers, then a + b is a unique. Closure property holds for addition and multiplication of whole numbers. What is the closure property?
Closure property holds for addition and multiplication of whole numbers. In mathematics, closure refers to the likelihood of an operation on elements of a set. What is the closure property? Closure property of whole numbers under addition: The closure property of addition for real numbers states that if a and b are real numbers, then a + b is a unique. If something is closed, then it means if an operation is.
Closure Property Of Addition Definition slidesharetrick
If something is closed, then it means if an operation is. Closure property of whole numbers under addition: In mathematics, closure refers to the likelihood of an operation on elements of a set. The closure property of addition for real numbers states that if a and b are real numbers, then a + b is a unique. Closure property holds.
DefinitionClosure Property TopicsSummary of Closure Properties
Closure property of whole numbers under addition: The closure property of addition for real numbers states that if a and b are real numbers, then a + b is a unique. Closure property holds for addition and multiplication of whole numbers. What is the closure property? If something is closed, then it means if an operation is.
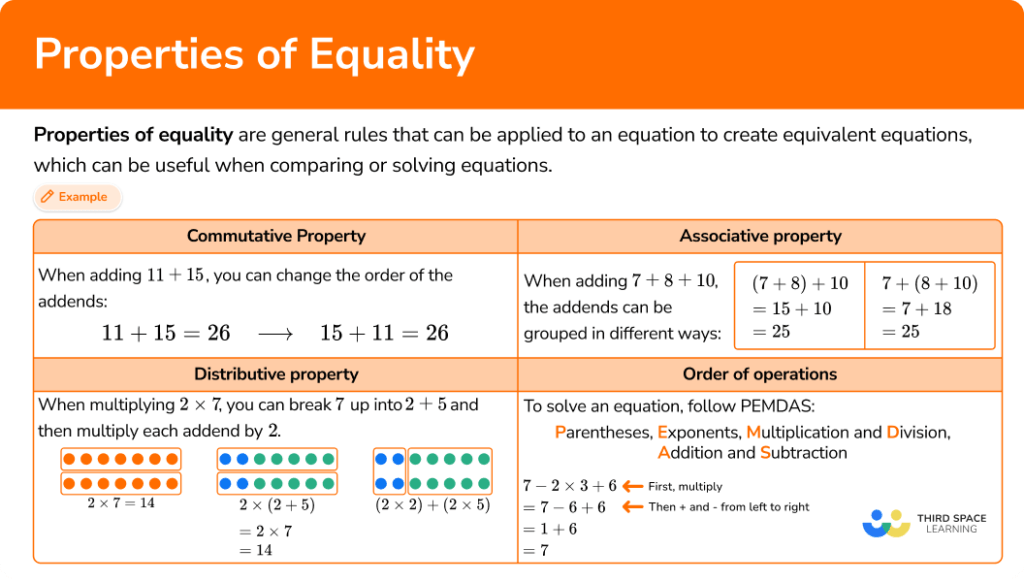
Properties of Equality Math Steps, Examples & Questions
Closure property holds for addition and multiplication of whole numbers. If something is closed, then it means if an operation is. Closure property of whole numbers under addition: What is the closure property? In mathematics, closure refers to the likelihood of an operation on elements of a set.
Algebra 1 2.01d The Closure Property YouTube
The closure property of addition for real numbers states that if a and b are real numbers, then a + b is a unique. In mathematics, closure refers to the likelihood of an operation on elements of a set. If something is closed, then it means if an operation is. What is the closure property? Closure property holds for addition.
Properties of Integers Closure Property MathsMD
What is the closure property? Closure property holds for addition and multiplication of whole numbers. If something is closed, then it means if an operation is. Closure property of whole numbers under addition: The closure property of addition for real numbers states that if a and b are real numbers, then a + b is a unique.
Closure Property Of Addition Definition slidesharetrick
What is the closure property? The closure property of addition for real numbers states that if a and b are real numbers, then a + b is a unique. Closure property holds for addition and multiplication of whole numbers. If something is closed, then it means if an operation is. In mathematics, closure refers to the likelihood of an operation.
8 Math Rational numbers Closure property YouTube
Closure property of whole numbers under addition: The closure property of addition for real numbers states that if a and b are real numbers, then a + b is a unique. What is the closure property? In mathematics, closure refers to the likelihood of an operation on elements of a set. If something is closed, then it means if an.
DefinitionClosure Property Media4Math
If something is closed, then it means if an operation is. What is the closure property? The closure property of addition for real numbers states that if a and b are real numbers, then a + b is a unique. Closure property of whole numbers under addition: In mathematics, closure refers to the likelihood of an operation on elements of.
DefinitionClosure Property TopicsReal Numbers and Closure Division
Closure property holds for addition and multiplication of whole numbers. If something is closed, then it means if an operation is. The closure property of addition for real numbers states that if a and b are real numbers, then a + b is a unique. Closure property of whole numbers under addition: In mathematics, closure refers to the likelihood of.
Closure of Relations (Solved Problems) Set 2 YouTube
Closure property of whole numbers under addition: In mathematics, closure refers to the likelihood of an operation on elements of a set. Closure property holds for addition and multiplication of whole numbers. If something is closed, then it means if an operation is. What is the closure property?
Closure Property Holds For Addition And Multiplication Of Whole Numbers.
Closure property of whole numbers under addition: What is the closure property? In mathematics, closure refers to the likelihood of an operation on elements of a set. If something is closed, then it means if an operation is.