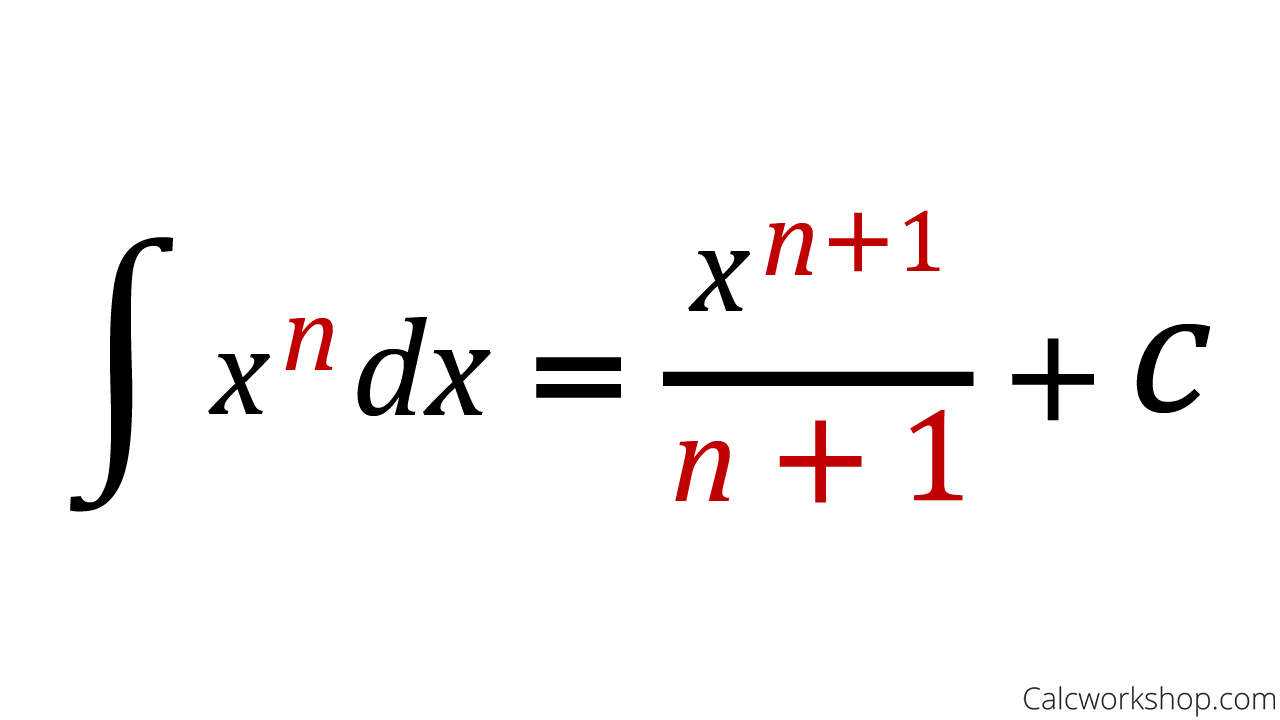Integration Math Rules - In this chapter we will give an introduction to definite and indefinite integrals. We will discuss the definition and properties of. Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution. Some important rules of integration are:
In this chapter we will give an introduction to definite and indefinite integrals. Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution. Some important rules of integration are: We will discuss the definition and properties of.
Some important rules of integration are: In this chapter we will give an introduction to definite and indefinite integrals. Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution. We will discuss the definition and properties of.
Integration Rules (Simplifying Calculus Problems)
Some important rules of integration are: We will discuss the definition and properties of. In this chapter we will give an introduction to definite and indefinite integrals. Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution.
Integration Cuemath
Some important rules of integration are: In this chapter we will give an introduction to definite and indefinite integrals. We will discuss the definition and properties of. Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution.
Antiderivative Rules
Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution. We will discuss the definition and properties of. Some important rules of integration are: In this chapter we will give an introduction to definite and indefinite integrals.
Integration Rules and Integration definition with examples Studypivot
In this chapter we will give an introduction to definite and indefinite integrals. We will discuss the definition and properties of. Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution. Some important rules of integration are:
Integration Rules What are Integration Rules? Examples
Some important rules of integration are: In this chapter we will give an introduction to definite and indefinite integrals. We will discuss the definition and properties of. Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution.
Integration Rules
In this chapter we will give an introduction to definite and indefinite integrals. We will discuss the definition and properties of. Some important rules of integration are: Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution.
What Is Calculus? Integration Rules and Examples Owlcation
Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution. In this chapter we will give an introduction to definite and indefinite integrals. Some important rules of integration are: We will discuss the definition and properties of.
Integration Rules
Some important rules of integration are: We will discuss the definition and properties of. In this chapter we will give an introduction to definite and indefinite integrals. Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution.
Cambridge AS Level Mathematics 9709 (Pure Mathematics 1) Revision
Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution. Some important rules of integration are: We will discuss the definition and properties of. In this chapter we will give an introduction to definite and indefinite integrals.
Integration Formula Examples List of Integration Formulas
We will discuss the definition and properties of. Some important rules of integration are: In this chapter we will give an introduction to definite and indefinite integrals. Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution.
We Will Discuss The Definition And Properties Of.
Sum rule \int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx add a constant to the solution. Some important rules of integration are: In this chapter we will give an introduction to definite and indefinite integrals.