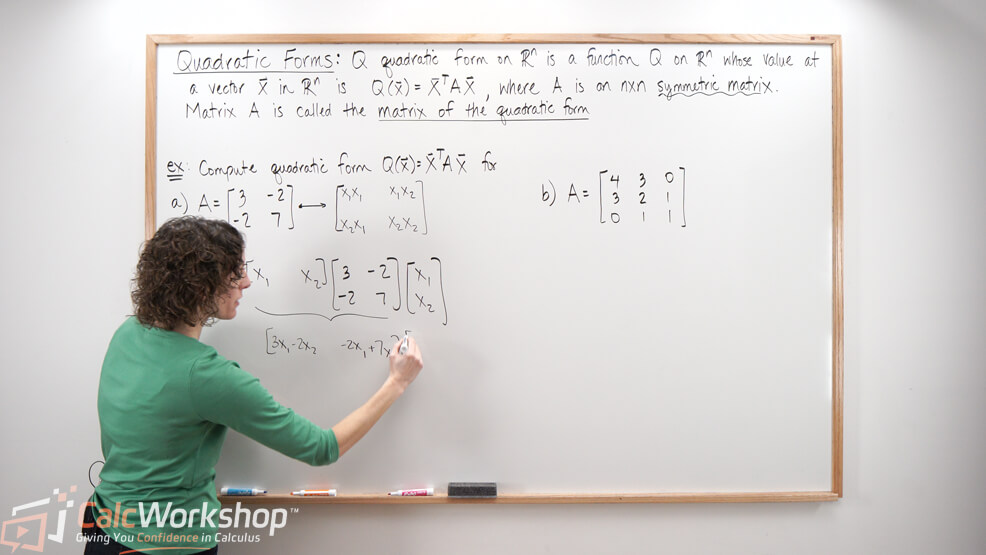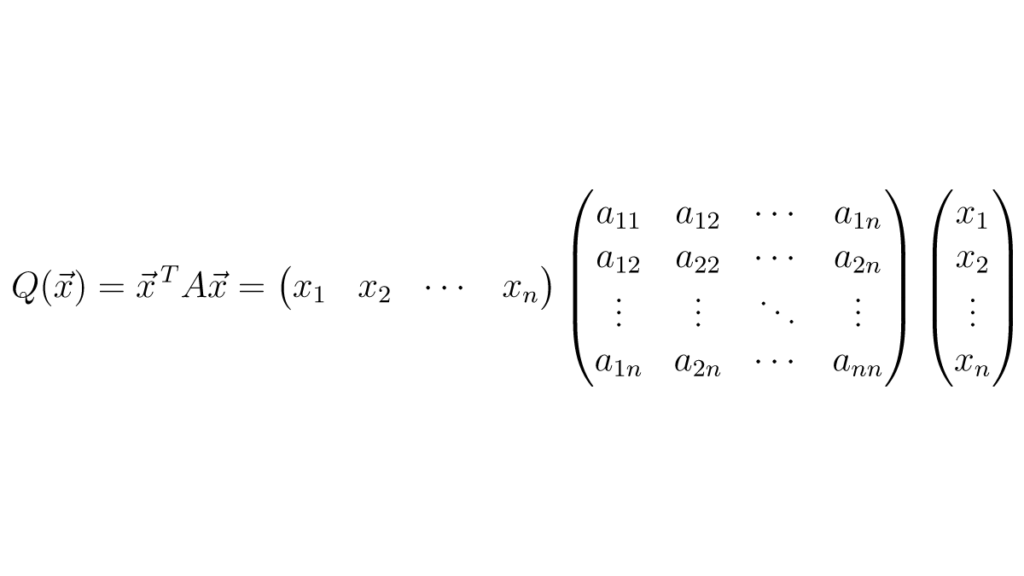Quadratic Form Matrix - See examples of geometric interpretation, change of. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. The quadratic form q(x) involves a matrix a and a vector x. The quadratic forms of a matrix comes up often in statistical applications. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. We can use this to define a quadratic form,. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. In this chapter, you will learn about the quadratic forms of a matrix. The matrix a is typically symmetric, meaning a t = a, and it determines.
The quadratic form q(x) involves a matrix a and a vector x. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. In this chapter, you will learn about the quadratic forms of a matrix. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. See examples of geometric interpretation, change of. We can use this to define a quadratic form,. The quadratic forms of a matrix comes up often in statistical applications. The matrix a is typically symmetric, meaning a t = a, and it determines.
The quadratic forms of a matrix comes up often in statistical applications. We can use this to define a quadratic form,. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. See examples of geometric interpretation, change of. The quadratic form q(x) involves a matrix a and a vector x. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. The matrix a is typically symmetric, meaning a t = a, and it determines. In this chapter, you will learn about the quadratic forms of a matrix. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no.
Quadratic form Matrix form to Quadratic form Examples solved
Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. The quadratic form q(x) involves a matrix a and a vector x. We can use this to define a quadratic form,. The matrix a is typically symmetric, meaning a t = a, and it determines..
Quadratic Form (Matrix Approach for Conic Sections)
The quadratic forms of a matrix comes up often in statistical applications. In this chapter, you will learn about the quadratic forms of a matrix. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. We can use this to define a quadratic form,. The matrix a is typically symmetric, meaning a t = a, and.
Solved (1 point) Write the matrix of the quadratic form Q(x,
The quadratic form q(x) involves a matrix a and a vector x. The quadratic forms of a matrix comes up often in statistical applications. Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. The matrix a is typically symmetric, meaning a t = a, and.
Linear Algebra Quadratic Forms YouTube
Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. In this chapter, you will learn about the quadratic forms of a matrix. The quadratic form q(x) involves a matrix a and a vector x. We can use this to define a quadratic form,. Recall that.
Quadratic Forms YouTube
Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. The quadratic forms of a matrix comes up often in statistical applications. See examples of geometric interpretation, change of. The quadratic.
SOLVEDExpress the quadratic equation in the matr…
Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. The matrix a is typically symmetric, meaning a t = a, and it determines. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m.
9.1 matrix of a quad form
The matrix a is typically symmetric, meaning a t = a, and it determines. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. In this chapter, you will learn about the quadratic forms of a matrix. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a.
PPT Quadratic Forms, Characteristic Roots and Characteristic Vectors
Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. The matrix a is typically symmetric, meaning a t = a, and it determines. The quadratic forms of a matrix comes up often in statistical applications. The quadratic form q(x) involves a matrix a and a vector x. In this chapter, you will learn about the.
Definiteness of Hermitian Matrices Part 1/4 "Quadratic Forms" YouTube
Find a matrix \(q\) so that the change of coordinates \(\mathbf y = q^t\mathbf x\) transforms the quadratic form into one that has no. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. In this chapter, you will learn about the quadratic forms of.
Representing a Quadratic Form Using a Matrix Linear Combinations
The quadratic forms of a matrix comes up often in statistical applications. The matrix a is typically symmetric, meaning a t = a, and it determines. In this chapter, you will learn about the quadratic forms of a matrix. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. Recall that a bilinear form from r2m.
Find A Matrix \(Q\) So That The Change Of Coordinates \(\Mathbf Y = Q^t\Mathbf X\) Transforms The Quadratic Form Into One That Has No.
The matrix a is typically symmetric, meaning a t = a, and it determines. Recall that a bilinear form from r2m → r can be written f(x, y) = xt ay where a is an m × m matrix. Learn how to define, compute and interpret quadratic forms as functions of symmetric matrices. See examples of geometric interpretation, change of.
The Quadratic Forms Of A Matrix Comes Up Often In Statistical Applications.
The quadratic form q(x) involves a matrix a and a vector x. In this chapter, you will learn about the quadratic forms of a matrix. We can use this to define a quadratic form,.