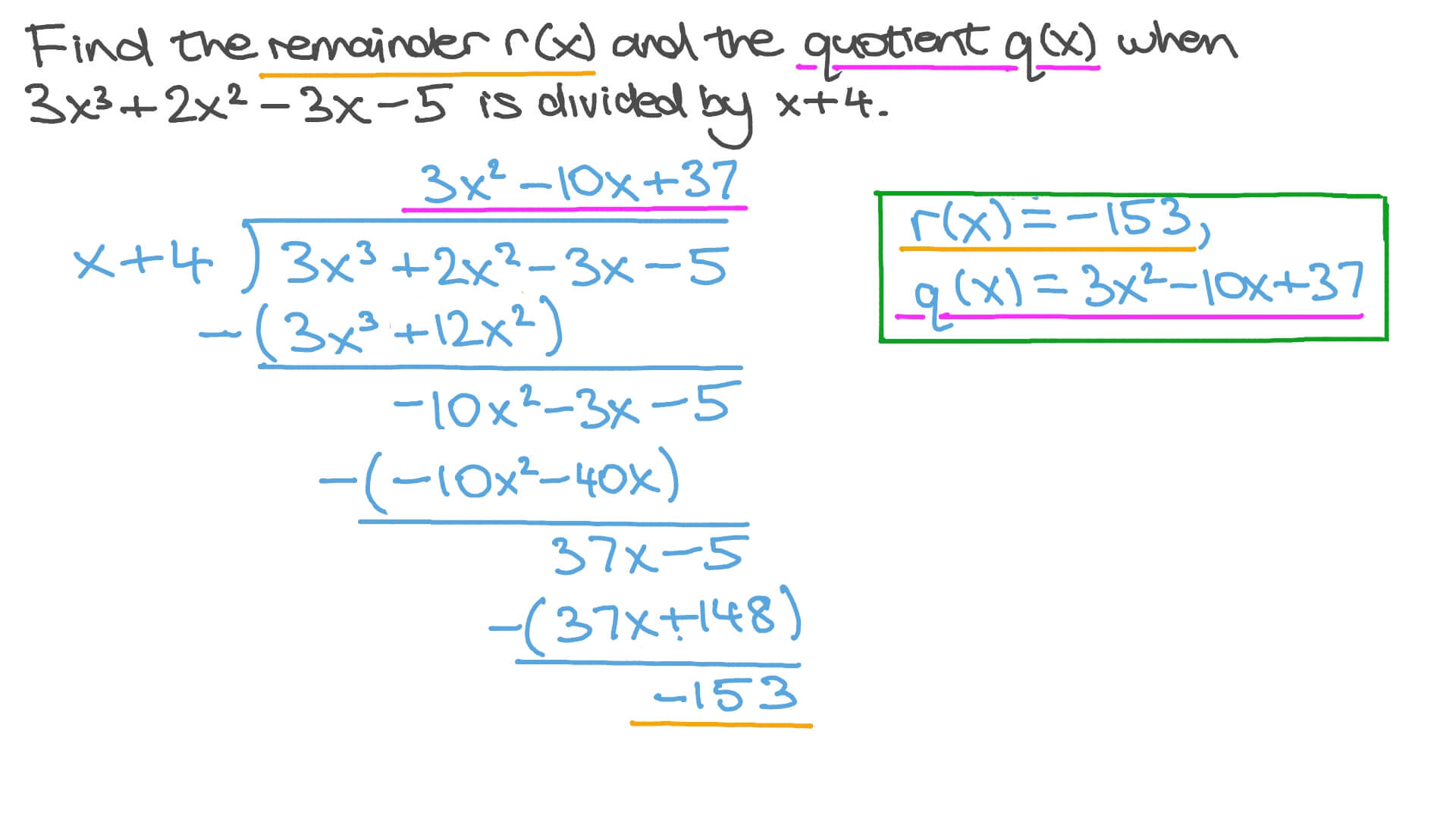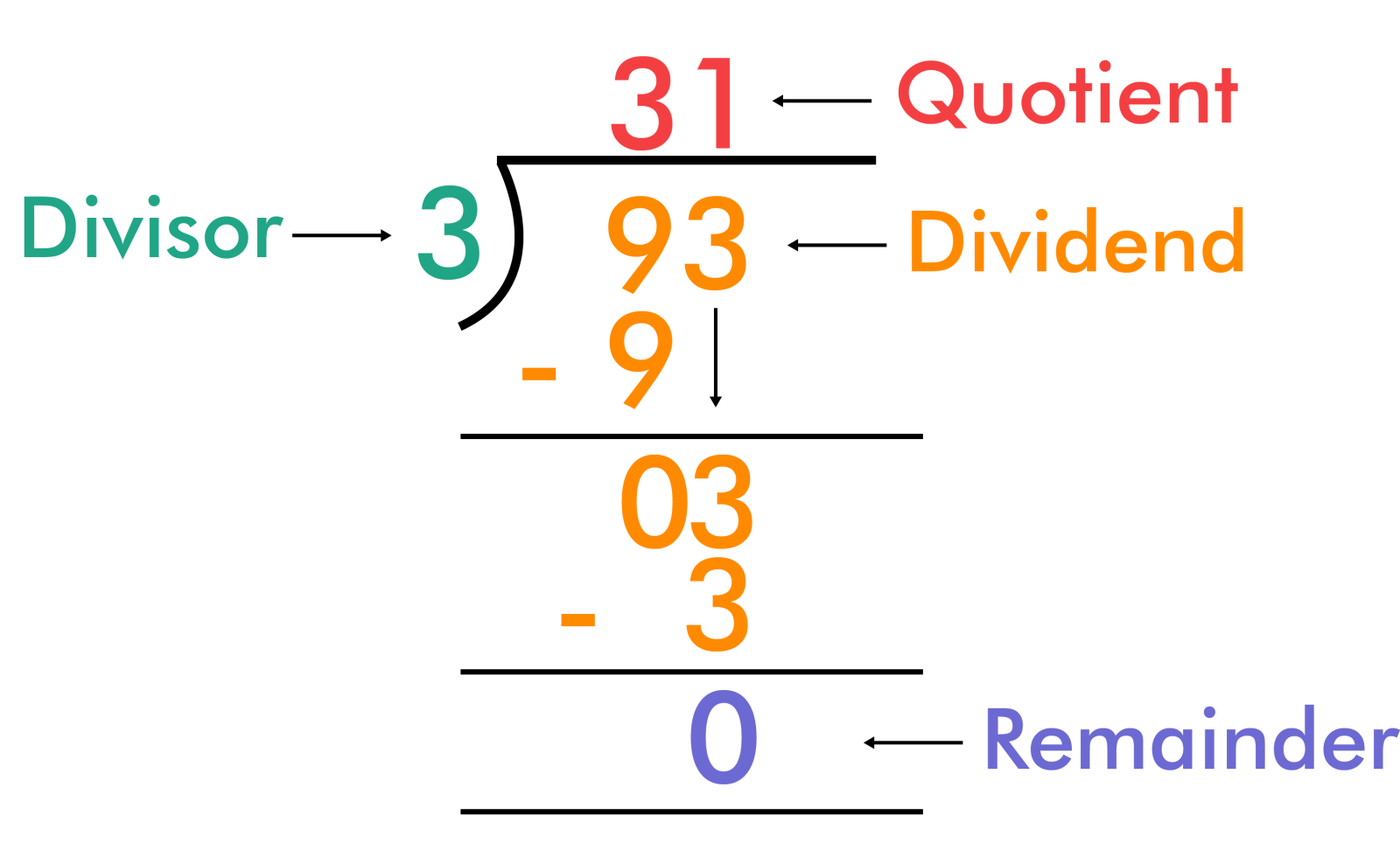Quotient Remainder Form - Given any integer n and a positive integer d, there exist unique integers q and r such that: N = d⋅q + r, and 0 ≤ r <. Quotient function given two integers a , b ∈ ℤ such that b ≠ 0 , then we get some q , r ∈ ℤ with 0 ≤ r < | b | such that a = b · q + r and we define a / / b : When dividends are not split evenly by the divisor, then the leftover part is the remainder. When we divide 13 ÷ 4, the remainder is.
When we divide 13 ÷ 4, the remainder is. Quotient function given two integers a , b ∈ ℤ such that b ≠ 0 , then we get some q , r ∈ ℤ with 0 ≤ r < | b | such that a = b · q + r and we define a / / b : When dividends are not split evenly by the divisor, then the leftover part is the remainder. Given any integer n and a positive integer d, there exist unique integers q and r such that: N = d⋅q + r, and 0 ≤ r <.
When we divide 13 ÷ 4, the remainder is. Quotient function given two integers a , b ∈ ℤ such that b ≠ 0 , then we get some q , r ∈ ℤ with 0 ≤ r < | b | such that a = b · q + r and we define a / / b : N = d⋅q + r, and 0 ≤ r <. Given any integer n and a positive integer d, there exist unique integers q and r such that: When dividends are not split evenly by the divisor, then the leftover part is the remainder.
The Remainder Theorem Top Online General
When dividends are not split evenly by the divisor, then the leftover part is the remainder. When we divide 13 ÷ 4, the remainder is. Given any integer n and a positive integer d, there exist unique integers q and r such that: Quotient function given two integers a , b ∈ ℤ such that b ≠ 0 , then.
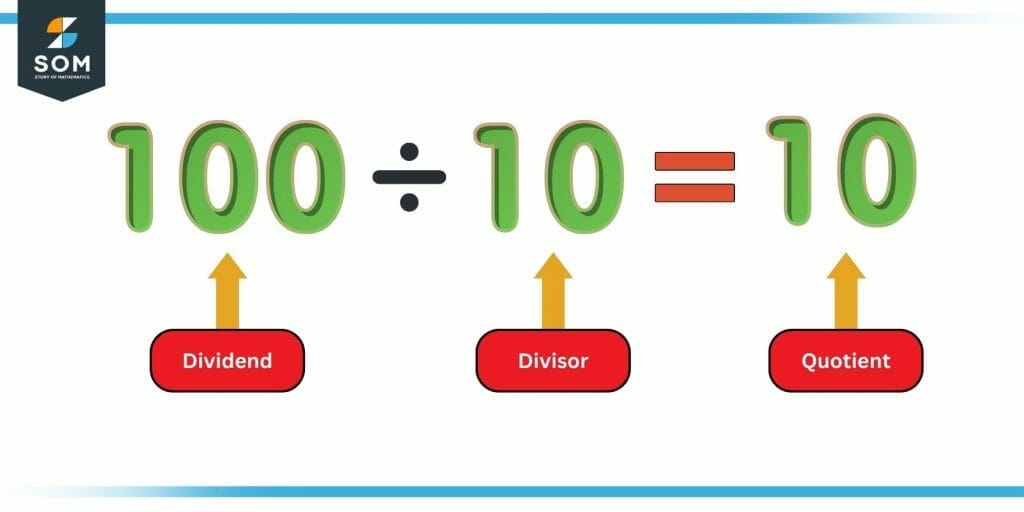
Quotient Definition & Meaning
Quotient function given two integers a , b ∈ ℤ such that b ≠ 0 , then we get some q , r ∈ ℤ with 0 ≤ r < | b | such that a = b · q + r and we define a / / b : When we divide 13 ÷ 4, the remainder is. Given.
How to write it in quotient + remainder/divisor form
Quotient function given two integers a , b ∈ ℤ such that b ≠ 0 , then we get some q , r ∈ ℤ with 0 ≤ r < | b | such that a = b · q + r and we define a / / b : N = d⋅q + r, and 0 ≤ r <..
Remainder Definition, Facts & Examples
When we divide 13 ÷ 4, the remainder is. N = d⋅q + r, and 0 ≤ r <. When dividends are not split evenly by the divisor, then the leftover part is the remainder. Given any integer n and a positive integer d, there exist unique integers q and r such that: Quotient function given two integers a ,.
Question Video Finding a Quotient and Remainder from a Polynomial
When dividends are not split evenly by the divisor, then the leftover part is the remainder. When we divide 13 ÷ 4, the remainder is. Given any integer n and a positive integer d, there exist unique integers q and r such that: Quotient function given two integers a , b ∈ ℤ such that b ≠ 0 , then.
What is a Remainder in Math? (Definition, Examples) BYJUS
Quotient function given two integers a , b ∈ ℤ such that b ≠ 0 , then we get some q , r ∈ ℤ with 0 ≤ r < | b | such that a = b · q + r and we define a / / b : When we divide 13 ÷ 4, the remainder is. When.
What is a Remainder in Math? (Definition, Examples) BYJUS
When we divide 13 ÷ 4, the remainder is. N = d⋅q + r, and 0 ≤ r <. When dividends are not split evenly by the divisor, then the leftover part is the remainder. Given any integer n and a positive integer d, there exist unique integers q and r such that: Quotient function given two integers a ,.
PPT Division of Polynomials PowerPoint Presentation ID272069
Given any integer n and a positive integer d, there exist unique integers q and r such that: When we divide 13 ÷ 4, the remainder is. Quotient function given two integers a , b ∈ ℤ such that b ≠ 0 , then we get some q , r ∈ ℤ with 0 ≤ r < | b |.
Writing Polynomials in (Divisor)(Quotient) + Remainder Form
Quotient function given two integers a , b ∈ ℤ such that b ≠ 0 , then we get some q , r ∈ ℤ with 0 ≤ r < | b | such that a = b · q + r and we define a / / b : N = d⋅q + r, and 0 ≤ r <..
Division With Remainders Examples
When we divide 13 ÷ 4, the remainder is. Given any integer n and a positive integer d, there exist unique integers q and r such that: When dividends are not split evenly by the divisor, then the leftover part is the remainder. N = d⋅q + r, and 0 ≤ r <. Quotient function given two integers a ,.
Given Any Integer N And A Positive Integer D, There Exist Unique Integers Q And R Such That:
When we divide 13 ÷ 4, the remainder is. Quotient function given two integers a , b ∈ ℤ such that b ≠ 0 , then we get some q , r ∈ ℤ with 0 ≤ r < | b | such that a = b · q + r and we define a / / b : When dividends are not split evenly by the divisor, then the leftover part is the remainder. N = d⋅q + r, and 0 ≤ r <.