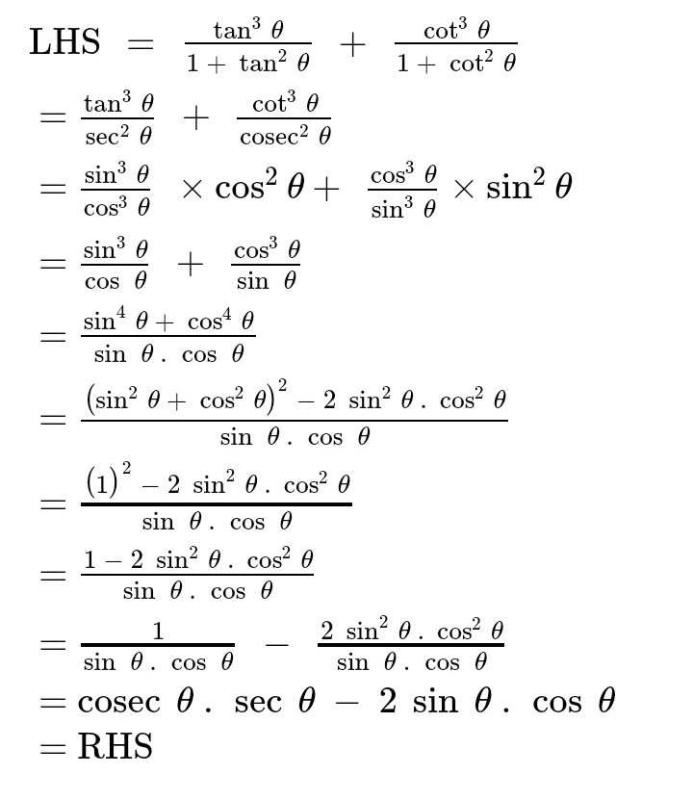Tan Theta To Cos Theta

Tan Theta To Cos Theta - Given sinθ = 116 and secθ>0 , how do you find cosθ,tanθ ? Then, write the equation in a standard form, and isolate the. Sin (θ) = opposite / hypotenuse. ⇒ sinθ = ± √1 −. ∙ xtanθ = sinθ cosθ. Cos (θ) = adjacent / hypotenuse. To solve a trigonometric simplify the equation using trigonometric identities. ∙ xsin2θ +cos2θ = 1. \displaystyle {\cos {\theta}}=\frac {\sqrt { {85}}} { {11}} and \displaystyle {\tan. For a right triangle with an angle θ :

To solve a trigonometric simplify the equation using trigonometric identities. Cos (θ) = adjacent / hypotenuse. \displaystyle {\cos {\theta}}=\frac {\sqrt { {85}}} { {11}} and \displaystyle {\tan. ⇒ sinθ = ± √1 −. Sin (θ) = opposite / hypotenuse. ∙ xsin2θ +cos2θ = 1. ∙ xtanθ = sinθ cosθ. Rewrite tan(θ)cos(θ) tan (θ) cos (θ) in terms of sines and cosines. Then, write the equation in a standard form, and isolate the. In trigonometry formulas, we will learn all the basic formulas based on trigonometry ratios (sin,cos, tan) and identities as per class.

∙ xsin2θ +cos2θ = 1. Express tan θ in terms of cos θ? \displaystyle {\cos {\theta}}=\frac {\sqrt { {85}}} { {11}} and \displaystyle {\tan. Cos (θ) = adjacent / hypotenuse. Sin (θ) = opposite / hypotenuse. For a right triangle with an angle θ : In trigonometry formulas, we will learn all the basic formulas based on trigonometry ratios (sin,cos, tan) and identities as per class. ∙ xtanθ = sinθ cosθ. To solve a trigonometric simplify the equation using trigonometric identities. Then, write the equation in a standard form, and isolate the.

Prove that ` (sin theta "cosec" theta )(cos theta sec theta )=(1

For a right triangle with an angle θ : Then, write the equation in a standard form, and isolate the. Rewrite tan(θ)cos(θ) tan (θ) cos (θ) in terms of sines and cosines. ⇒ sinθ = ± √1 −. ∙ xtanθ = sinθ cosθ.

tan theta/1cot theta + cot theta/1tan theta= 1+ sec theta cosec theta

Given sinθ = 116 and secθ>0 , how do you find cosθ,tanθ ? Cos (θ) = adjacent / hypotenuse. ∙ xsin2θ +cos2θ = 1. To solve a trigonometric simplify the equation using trigonometric identities. In trigonometry formulas, we will learn all the basic formulas based on trigonometry ratios (sin,cos, tan) and identities as per class.

$\4.Provethat\frac{\tan \theta}{1\tan \theta}\frac{\cot \theta}{1\cot$

\4.Provethat\frac{\tan \theta}{1\tan \theta}\frac{\cot \theta}{1\cot

⇒ sinθ = ± √1 −. Given sinθ = 116 and secθ>0 , how do you find cosθ,tanθ ? Rewrite tan(θ)cos(θ) tan (θ) cos (θ) in terms of sines and cosines. Then, write the equation in a standard form, and isolate the. ∙ xtanθ = sinθ cosθ.

$=\frac{\sin \theta(1+\cos \theta)+\tan \theta(1\cos \theta)}{(1\cos \th..$

=\frac{\sin \theta(1+\cos \theta)+\tan \theta(1\cos \theta)}{(1\cos \th..

Sin (θ) = opposite / hypotenuse. In trigonometry formulas, we will learn all the basic formulas based on trigonometry ratios (sin,cos, tan) and identities as per class. ∙ xtanθ = sinθ cosθ. Given sinθ = 116 and secθ>0 , how do you find cosθ,tanθ ? Cos (θ) = adjacent / hypotenuse.

Find the exact expressions for sin theta, cos theta, and tan theta. sin

For a right triangle with an angle θ : ⇒ sinθ = ± √1 −. Given sinθ = 116 and secθ>0 , how do you find cosθ,tanθ ? Express tan θ in terms of cos θ? \displaystyle {\cos {\theta}}=\frac {\sqrt { {85}}} { {11}} and \displaystyle {\tan.

画像 prove that tan^2 theta/1 tan^2 theta 298081Prove that cos 2 theta

Rewrite tan(θ)cos(θ) tan (θ) cos (θ) in terms of sines and cosines. ⇒ sinθ = ± √1 −. For a right triangle with an angle θ : In trigonometry formulas, we will learn all the basic formulas based on trigonometry ratios (sin,cos, tan) and identities as per class. ∙ xtanθ = sinθ cosθ.

Tan thetacot theta =0 then find the value of sin theta +cos theta

Cos (θ) = adjacent / hypotenuse. Sin (θ) = opposite / hypotenuse. ⇒ sinθ = ± √1 −. For a right triangle with an angle θ : Given sinθ = 116 and secθ>0 , how do you find cosθ,tanθ ?

選択した画像 (tan^2 theta)/((sec theta1)^2)=(1 cos theta)/(1cos theta) 274439

Sin (θ) = opposite / hypotenuse. ∙ xtanθ = sinθ cosθ. To solve a trigonometric simplify the equation using trigonometric identities. \displaystyle {\cos {\theta}}=\frac {\sqrt { {85}}} { {11}} and \displaystyle {\tan. Given sinθ = 116 and secθ>0 , how do you find cosθ,tanθ ?

Tan Theta Formula, Definition , Solved Examples

∙ xtanθ = sinθ cosθ. Cos (θ) = adjacent / hypotenuse. Given sinθ = 116 and secθ>0 , how do you find cosθ,tanθ ? Express tan θ in terms of cos θ? Sin (θ) = opposite / hypotenuse.

tan theta+sec theta1/tan thetasec theta+1=1+sin theta/cos theta

⇒ sinθ = ± √1 −. For a right triangle with an angle θ : To solve a trigonometric simplify the equation using trigonometric identities. Then, write the equation in a standard form, and isolate the. Given sinθ = 116 and secθ>0 , how do you find cosθ,tanθ ?

Express Tan Θ In Terms Of Cos Θ?

To solve a trigonometric simplify the equation using trigonometric identities. ∙ xtanθ = sinθ cosθ. Sin (θ) = opposite / hypotenuse. Then, write the equation in a standard form, and isolate the.

Cos (Θ) = Adjacent / Hypotenuse.

Given sinθ = 116 and secθ>0 , how do you find cosθ,tanθ ? Rewrite tan(θ)cos(θ) tan (θ) cos (θ) in terms of sines and cosines. ⇒ sinθ = ± √1 −. ∙ xsin2θ +cos2θ = 1.